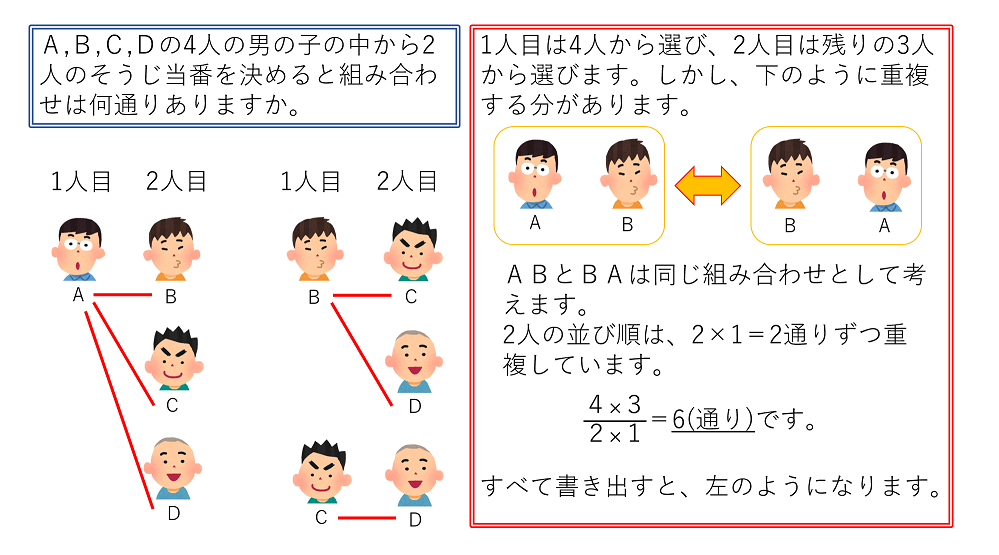
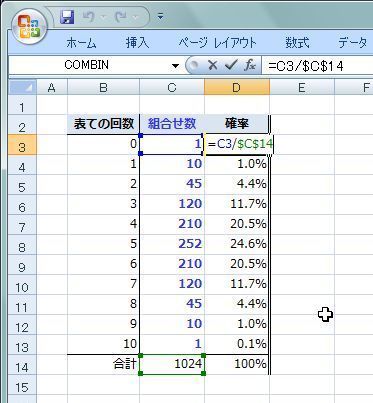
☆今、大きな話題になっているtoto*BIGですが、 この組合せが全部で何通りあるのか考えてみました。 ホームチームが勝てば1、負ければ2、延長とかそのほかが0です。 つまり1試合に3通り出る確率があります。 対象となる試合数は14試合なので、答えは以外に簡単でした。何通りありますか。 (2)遠回りせずにウを必ず通ってイに 行くのは何通りありますか。 (3)遠回りせずにウを通らないでイに 行くのは何通りありますか。では,組み合わせの問題を考えていくことにします。 例題3 男子2人,女子3人がいます。その中から,男子1人,女子2人を選ぶ選び方は何通りあるか。
組み合わせ C とは 公式や計算方法 は何通り 受験辞典
組み合わせ 何通り 計算
組み合わせ 何通り 計算-組み合わせではなく、「席の問題」となります。 答え:まず10人の中から委員長を選び、 残った9人の中から副委員長を選ぶので、 `10xx9=90` 通り // 例3)5題の問題に 、×で答える答え方は何通りあ組み合わせは、順序に意味がある順列とは異なります。 総数 = n、抜き取り数 = r とすると、組み合わせの総数は、次の数式で表されます。 問題3それぞれA,B,Cと書かれたカードがあります。




場合の数 色の組み合わせは何通り Youtube
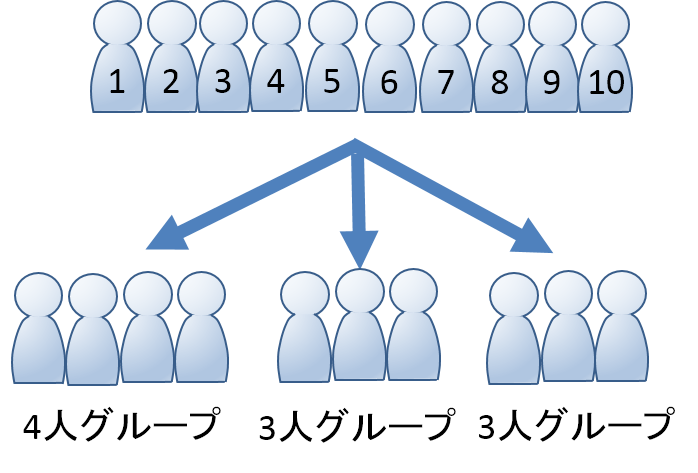
= 6 C 4 \dfrac{6!}{4!2!}={}_6\mathrm{C}_4 4 !6人の生徒を3組に分ける方法は,全部で何通りありますかただし,どの組にも少なくとも1人の生徒がいるものとします 10 15 60 70 90 105 140 210 280 560 松谷です。 16人トーナメントの組み方は何通りか? 小学生部の授業中に、中学生から質問されて結構適当に答えてしまったので懺悔のためにブログにしておきます。 まず、ちょっと多すぎるので少ない4人のトーナメントから確認します。 こんなトーナメントがあって、この表の見え方と
Ex)6個の林檎を3人に分配する方法は何通りか。ただし1個も貰わない人がいてもよいとする。 ただし1個も貰わない人がいてもよいとする。 解) 3人を A , B , C とし、この3人が貰うべき林檎に A , B , C とマジックで書き込んでいくことを考えれば、上述と 3!(通り)が今回は1(通り)と数えられるので、 (n1)通りと3!(通り)が対応します。 まとめると、 #1を解いて、6n=732⇔n=122(通り)// 例題(22)6人を区別のつかない3部屋に分ける場合の数を求めよ。但し空室があってはならないとする。ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。
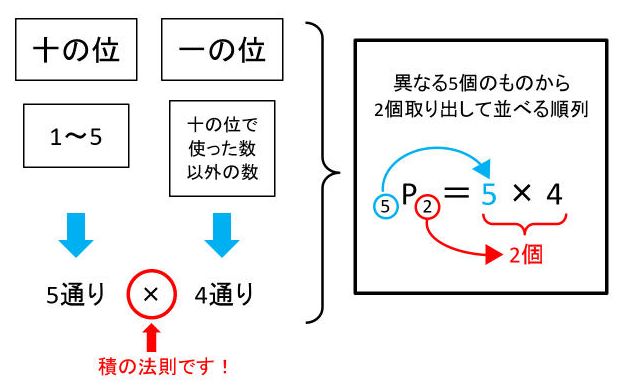
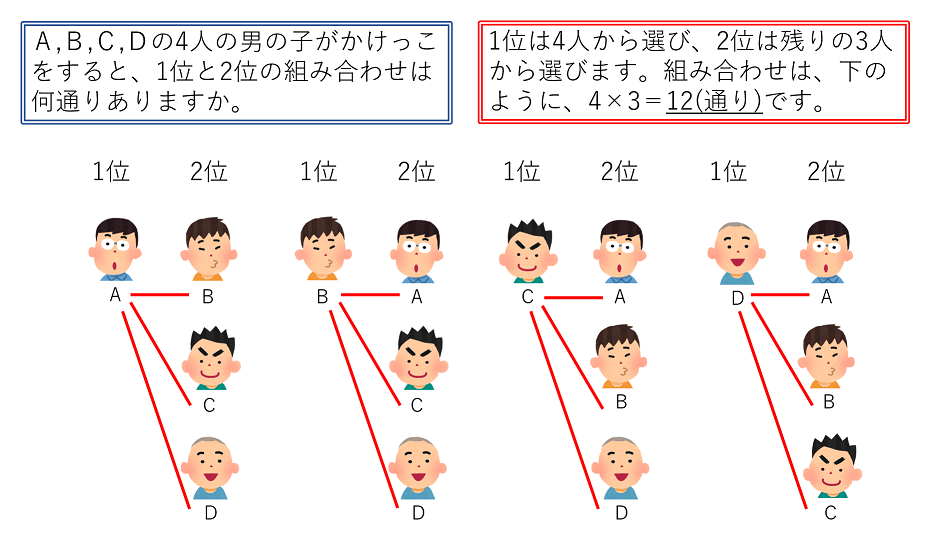
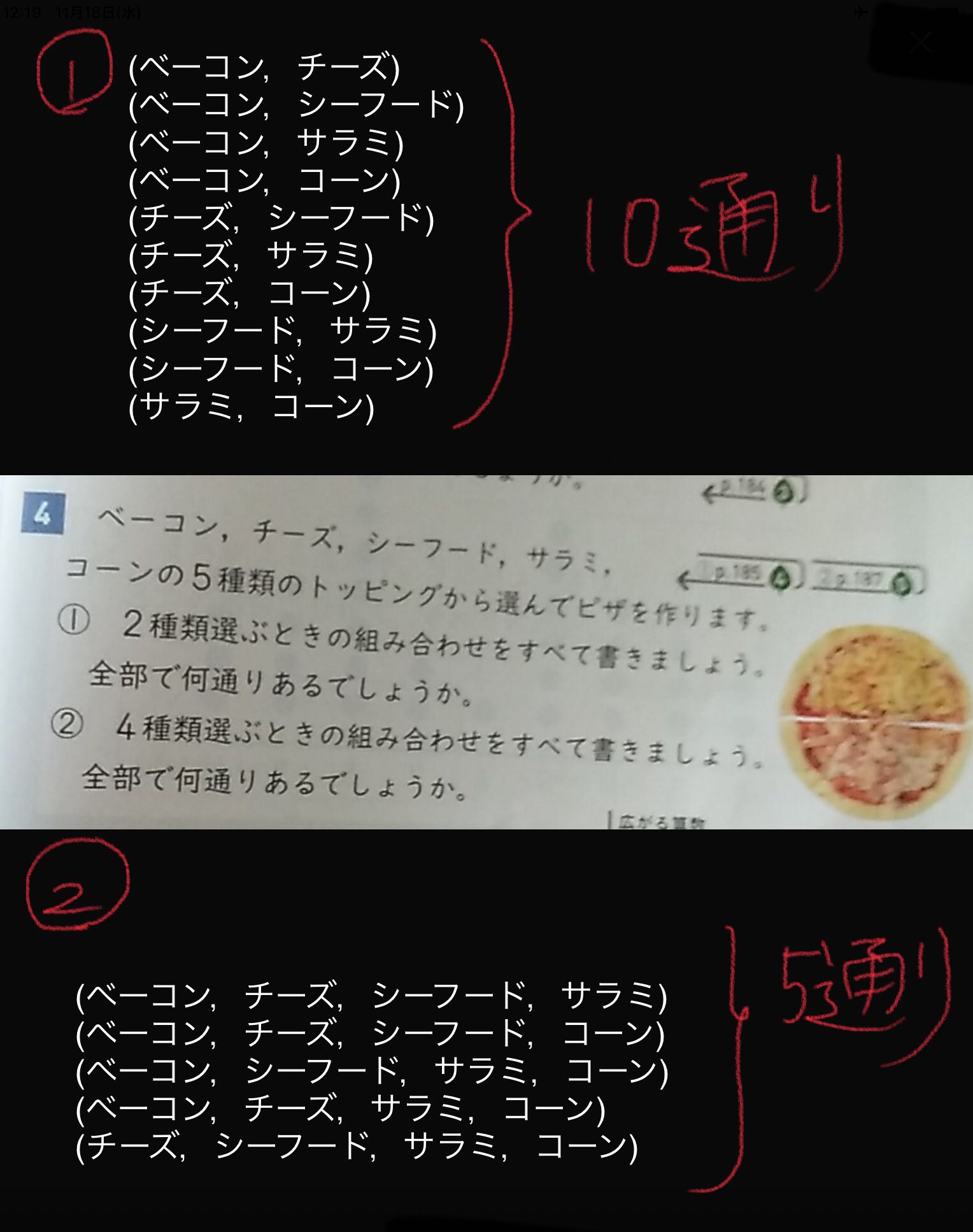
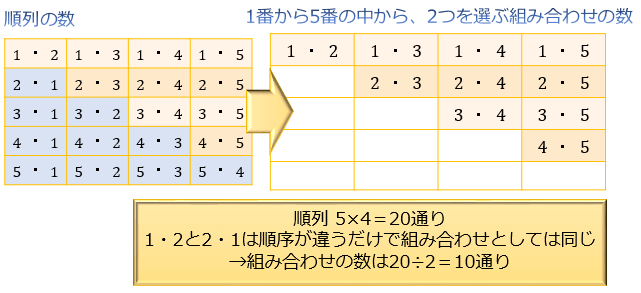
左図のトリニトロトルエンの異性体が何通りあるかという問題と同じです(自然界ではno 2 がch 3 に対して,2,4,6の位置にあるものしかできないらしいが,理屈上は何通りあるかと考えた場合).ch 3 を上端に固定して,hを並べていくとよいでしょう.この ①は 順列 で、答えは 5 P 2 =5×4=通り ②は 組み合わせ で、答えは 5 C 2 =5×4÷2=10通りになります。結局4 2 ×4 7 =4 9 通りの組み合わせがあります。 また「国士無双の13面待ち」の配牌は13種類の牌からなる配牌で、「」の形です。全ての牌はどの一枚を使うか4通りずつあるので、4 13 通りの組み合わせがあります。




Combin関数で組み合わせの数を求める Excel関数 できるネット
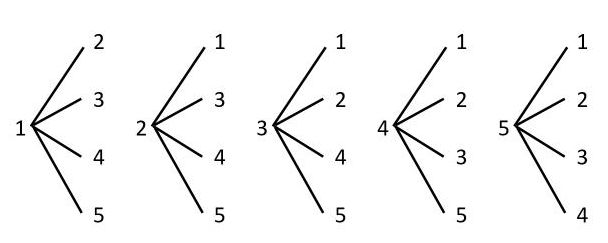



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
組み合わせは全何通り? 競艇は6艇で競われる競技のため、3連単の組み合わせは全部で1通り。 このことから、3連単が当たる確率は 08%(1/1) となり、的中させることが難しい玄人向けの買い方と言えるでしょう。 確率(的中率)の底上げは可能 2 配牌の形は何通りあるか 前提条件 牌は通常の34種類×4枚=136枚とします。 計算に影響する特殊な牌(花牌・白ポッチなど)は含まないものとします。 対応バージョン: 365 19 16 13 10 総数個の項目のなかから抜き取り数個を取り出したとき、何種類の組み合わせが可能であるかを求めます。
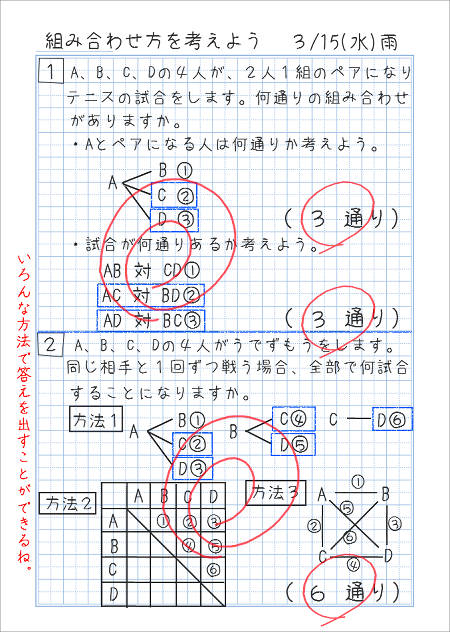



上何 通り ある か 計算 小学生 子供のための最高のぬりえ



トランプの組み合わせは全部で何通りあるのか News Magic More
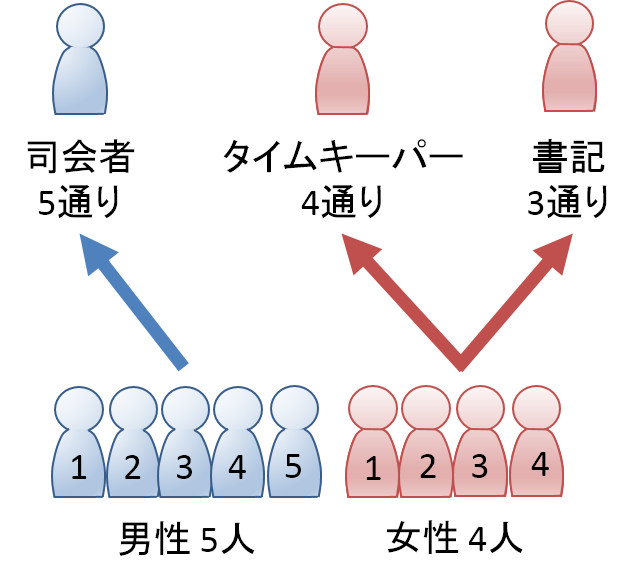
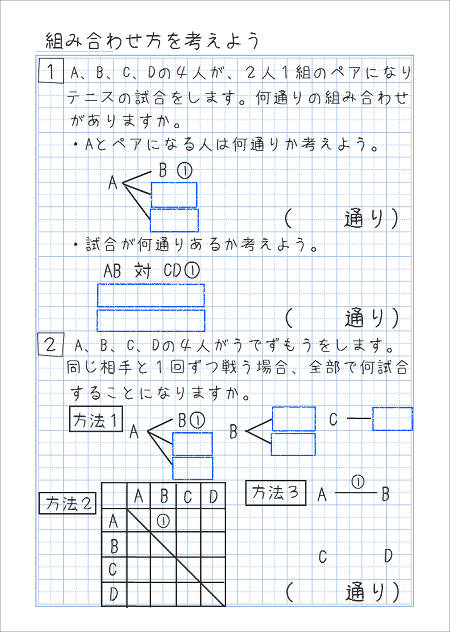
コインの組み合わせは何通り? 〜動的計画法〜 問題:1枚あたりの価値が{2,3,5}の3種類のコインを組み合わせ、金額の合計をちょうど14にするやり方は何通りか。コインはそれぞれ何枚でも使ってよいとする。 coin = 2 いろいろな組合せの問題 具体的な問題を通して,組合せの考え方に慣れましょう. 例題 男子 $5$ 人女子 $4$ 人から,男子 $2$ 人,女子 $2$ 人の委員を選ぶ方法は何通りあるか. 人は当然区別がつくものと考えます.まず,男子 $5$ 人から $2$ 人を選ぶ方法は,${}_5 \mathrm{C} _2=10$ 通りです.(選ぶ その組み合わせは4通り×4通りの16通りとなる。 実際に書き出してみると aa at ag ac tt ta tg tc gg ga gt gc cc ca ct cg の16通りだ。 まだ、種類には届かない。だが、考えの方向性はこれでよさそうだ。




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生
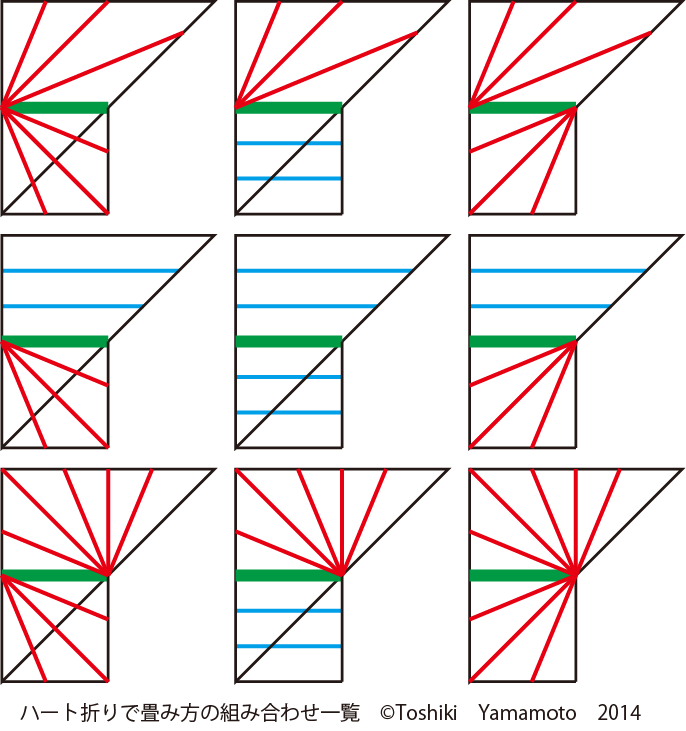



組合せ 何通り 一覧表 好きかも おりぞめ染伝人ブログ
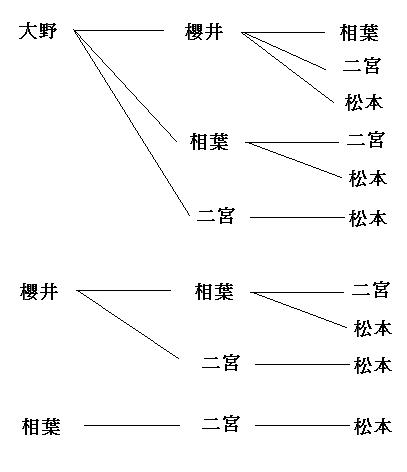
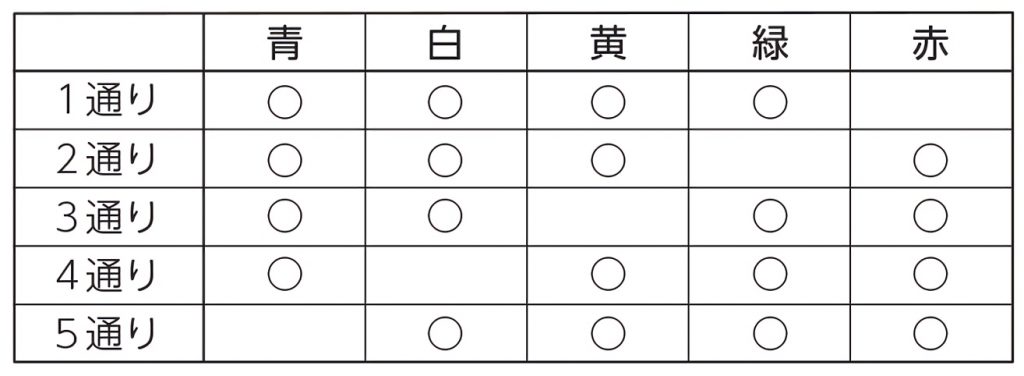
の8通りとなる.したがって総数は,14通りである. 5点の場合は,打たない1点の位置を考えれば6通りである. 6点の場合は1通りである. 以上より,その総数は, 1+7+15+14+6+1=44(通り) である 3仮名文字をみる例題 (1) 両親と子供 4 人の 6 人が円形のテーブルに向って座るとする。 次のような座り方は何通りあるか。 ( ア ) 6 人全体の座り方 ( イ ) 両親が隣り合わない座り方 ①異なる n 人 ( n 個 ) を並べる円順列は で求めよう。 ②隣り合わないときは余事象この中から4つ玉を選ぶときに得られる色のパターンが何通りあるか求めよ。 「三種類の玉から4つ選ぶ方法」と「 4つと仕切り2つを一列に並べる方法」は図のように1対1に対応するので,求める場合の数は 6 !



1
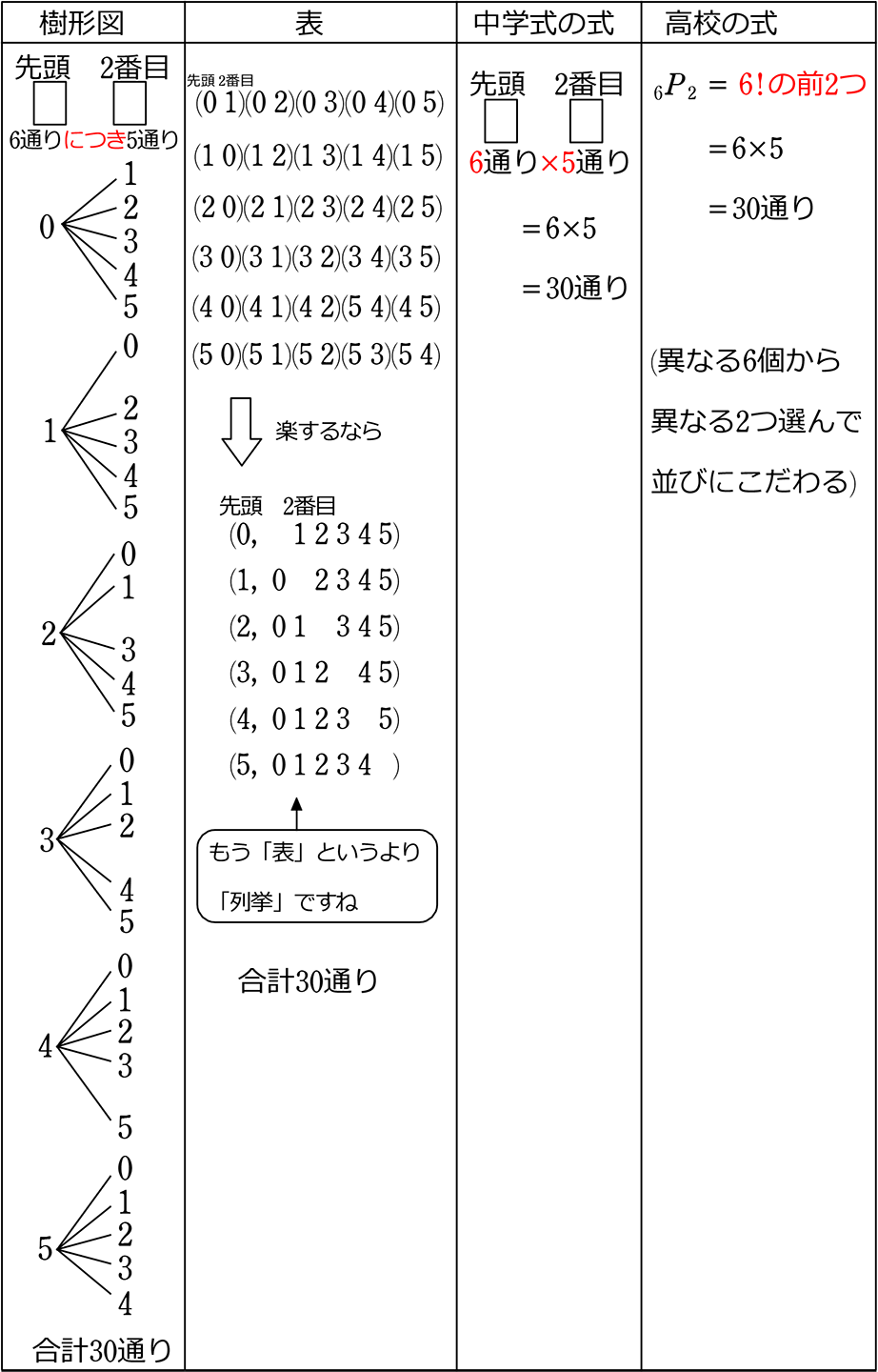



中学数学 場合の数
今回は、組み合わせパターンを調べる関数をご紹介します。 組み合わせパターンを調べる 例えば、14種類のデータがあったとして、その中から3つを1セットとした場合、全部で何通りのパターンが考えられるか? combin関数での引数の指定 総数:種類の何通りの並べ方があるか。 列の1番目:{a,b,c,d}から一つとるのだから、四通りの選び方がある。 列の2番目:{a,b,c,d}から一番目の選択を除いたものから、 一つとるのだから、 三通りの選び方がある。 今回はアルゴリズムと言うより、競技プログラミングのお題に近いです。 500 円玉を a 枚、100 円玉を b 枚、50 円玉を c枚持っているとします。これらの硬貨の中から何枚かを選び、合計金額をちょうど x 円となる方法は何通りあるでしょうか? 例えば、100円が何通りあるか調べたい




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
組合せ 友達がよくわからないことを言っていたので、調べてみた。 楽しかった。 一日1440分ある時刻から任意で12個抽出すると何通りあるかを調べた。 一日12本しか列車が来ないローカル線の駅の時刻表を見て、ふと思いついた。 桁数がとてつもなく 左端・右端の少なくとも一端がジョーカーになる並べ方は何通りでしょうか。 順列から組み合わせを求める ジョーカーを区別して数えて「順列」を求めた上で、 ジョーカーの重複度で割れば「組み合わせ」を求めることができます。 左端がジョーカーの場合



上何 通り ある か 計算 小学生 子供のための最高のぬりえ



2



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素



2n 8の場合 精子や卵細胞に入る染色体の組み合わせは何通りあるか Yahoo 知恵袋



数字の組み合わせの問題で 7人の中から3人選ぶ組み合わせは何通りあるのでし Yahoo 知恵袋



湘南理工学舎 初歩の数学 三角関数




Spi 数学 対策問題 組み合わせ 順列 しかくのいろは




場合の数 並べる と 選ぶ の計算方法の違い




高校数学 数a 14 組み合わせ 基本編 Youtube




中学数学 場合の数
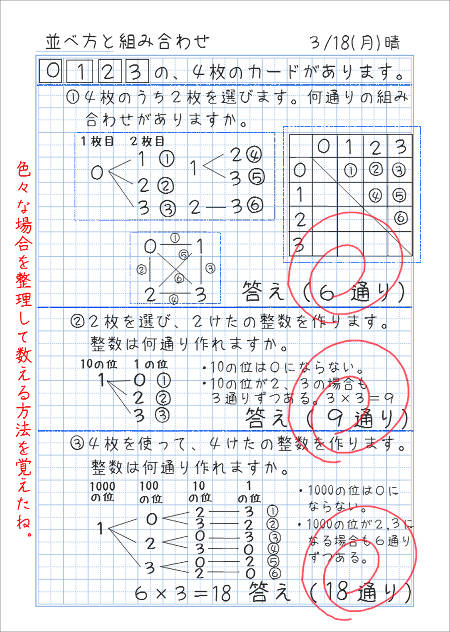



並べ方と組み合わせ方 その2 家庭学習レシピ




高校数学 数a 17 組合せ 道順編 Youtube
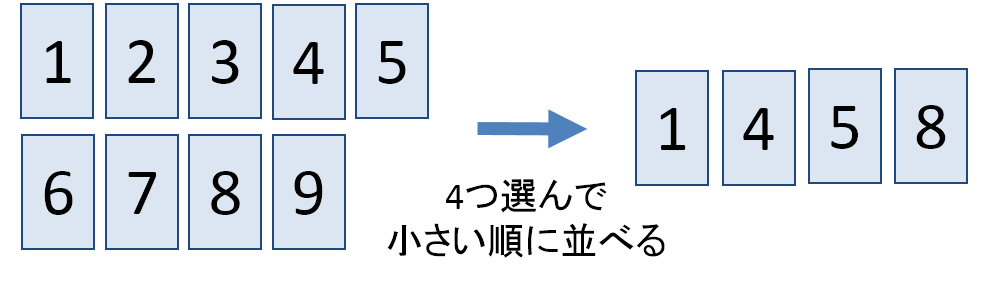



7 3 Cの使い方 統計学の時間 統計web



1



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




順列nprの計算 数学a フリー教材開発コミュニティ Ftext



Q Tbn And9gcrwcnbyjcxmrexvqio6nv6s L8p7sr Ptt0dbbh Tfkgamcgurj Usqp Cau




アルゴリズム コインの組み合わせは何通り Javascriptで実装する S Note




高校生と塾講師 家庭教師 のための数学 数 A 組み合わせ 道順 最短経路 縦3マス横4マスを左下aから右上bまでいく 最短経路は何通り あるか また 縦1横3のポイントcを必ず通過する場合は何通りか
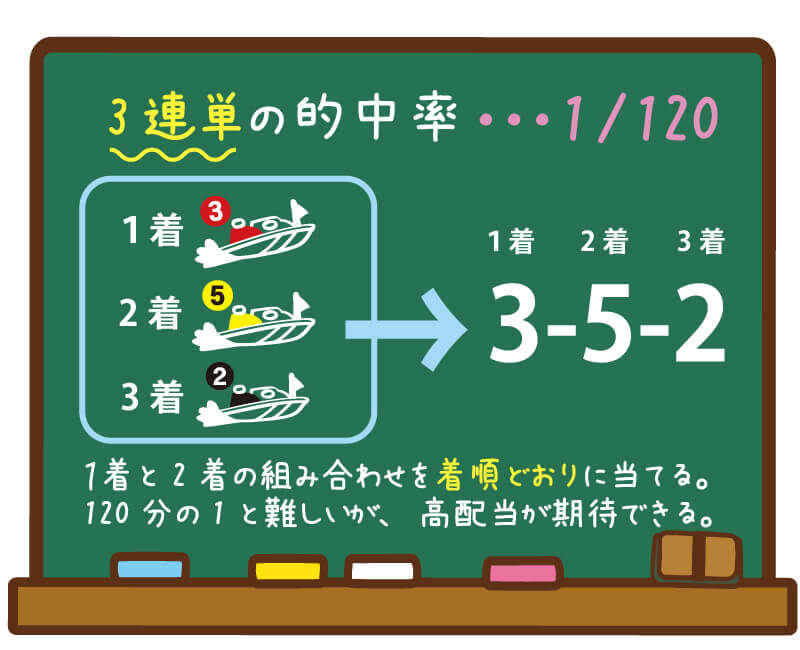



競艇の3連単とは全何通り 当たる確率や平均配当 勝てる買い方を考察 競艇マニア



7 2 Pの使い方 統計学の時間 統計web




組合せは1時間で解けるようになる 外資系コンサルタントが主夫になったら



湘南理工学舎 初歩の数学 三角関数




ロト7の組み合わせ数は全部で何通り 当たる確率や期待値は 宝くじ生活



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ



確率の問題です A B C D Eの5人から3人の委員を選ぶとき 何 Yahoo 知恵袋



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける



Q Tbn And9gctxdi2gahegsztlfoxxevlwukk864d1nmqfo1py86n T5pckgol Usqp Cau




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




Combin関数で組合せ 抜取り の数を求めてみた Excel 数学関数 Haku1569 Excel でらくらく データ分析
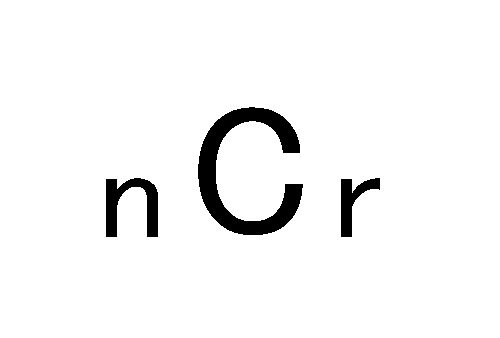



組み合わせの基本と計算方法 順列との違いを説明




の順列と の解き方を教えてほしいです Clear



上何 通り ある か 計算 小学生 子供のための最高のぬりえ



7 3 Cの使い方 統計学の時間 統計web




高校数学 数a 15 組合せ 文字編 Youtube




組み合わせ C とは 公式や計算方法 は何通り 受験辞典



組み合わせが何通りか調べる時に使う図の名前を教えてください A B Yahoo 知恵袋



組み合わせ 計算何通り 流し ボックス組合せ早見表 Mspk




トランプの並びは何通り 新しい組み合わせができる確率は 数学の面白いこと 役に立つことをまとめたサイト




ロト6の組み合わせ数は全部で何通り 当たる確率や期待値は 宝くじ生活




数1a 順列 組合せ 21 重複組合せ と を並べるやつ Youtube



5人から3人選ぶ組み合わせは 何通りですか また 式と考え方もお願い Yahoo 知恵袋



Combin関数で組合せ 抜取り の数を求めてみた Excel 数学関数 Haku1569 Excel でらくらく データ分析



順列と組み合わせの違いをリレーのチーム選考に例える コード7区




何通りも組み合わせが楽しめるバングル Happy Plus One ハピプラワン




赤玉 青玉 白玉が5個ずつ入った箱から5個の玉を取り出す 取り出し方の組み合わせは何 Clear



2




場合の数 色の組み合わせは何通り Youtube




中学受験算数 硬貨の組み合わせ 意外と難問です 毎日1題中学受験算数17 Youtube




ポーカーの確率 カードの組合せ総数と 各役の出現率



上何 通り ある か 計算 小学生 子供のための最高のぬりえ




順列と組み合わせ Alis



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



A B Cの組み合わせは8通りですが これは自分で書き出す以外どのよう Yahoo 知恵袋




3 3 A B C31 4 51 500 00 Descubre Como Resolverlo En Qanda



組み合わせ 計算何通り 流し ボックス組合せ早見表 Mspk




の倍数は何通りできるか問題 数学の偏差値を上げて合格を目指す




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




組み合わせは何通りもあるので飽きずに遊べます 大木のおもちゃ動物




小6算数 場合の数 2 指導アイデア みんなの教育技術




7 22 6 3 5 238 0 230 0 Descubre Como Resolverlo En Qanda




組み合わせは何通り For Android Apk Download



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




4桁の数字は何通りある 0 9や1 9の場合 6桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 ページ 2 2 中学受験ナビ



場合の数 学び家 Com




15 1 1 1 4 B C 3 Descubre Como Resolverlo En Qanda
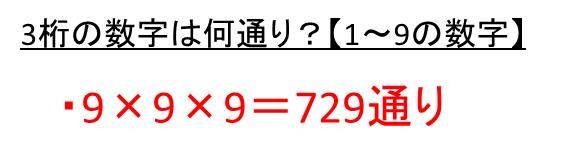



3桁の数字は何通りある 0 9や1 9の場合 5桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム
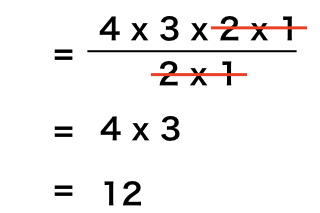



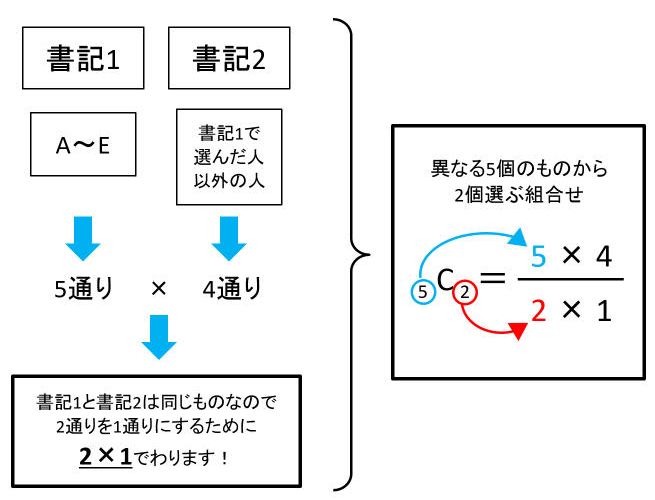
組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather




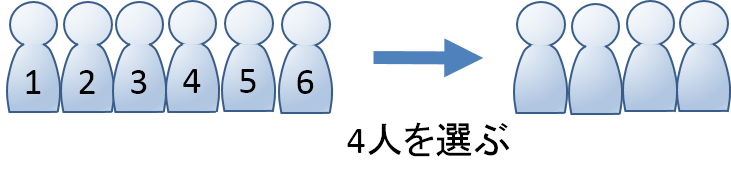
4人の中から2人選ぶ場合何通りの組み合わせがあるか 4人から3人選ぶ時は何通りか 5人から3人 4人を選ぶ場合何通りか 確率 More E Life




組み合わせは何通り For Android Apk Download



7 22 6 3 5 238 0 230 0 Descubre Como Resolverlo En Qanda



数学aの重複組合せで質問です 4種類の果物を6個買う時 何通りの買い方があるか Yahoo 知恵袋



小6算数 場合の数 2 指導アイデア みんなの教育技術




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




重複組合せ 同じものを何人かで分ける場合の数は何通りあるか みみずく戦略室




並べ方と組み合わせ方 その2 家庭学習レシピ




組み合わせ C とは 公式や計算方法 は何通り 受験辞典




この問題の組み合わせは何通りあるか教えてください Clear




Bar2 3 52 O 8 Right 5 X Descubre Como Resolverlo En Qanda




小6 算数 小6 40 並べ方 組み合わせ方 Youtube



2




小学生の算数全部で何通りですがわかりません 小学6年生の親です小学 数学 教えて Goo




ビンゴ5の組み合わせ数は全部で何通り 当たる確率や還元率は 宝くじ生活




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




通年 セット着用可 同素材で何通りも組み合わせが可能 ネイビー ユニバーサルランゲージ The タイトスカート Suit スカートスーツ ウォッシャブル 通年用 Company スーツ セットアップ ダブルサテン タイトスカート Outlet



7 3 Cの使い方 統計学の時間 統計web




何通りある 順列まとめ 数学の偏差値を上げて合格を目指す




頭がこんがらがります わかりやすいやり方とか教えて下さい W Clear



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
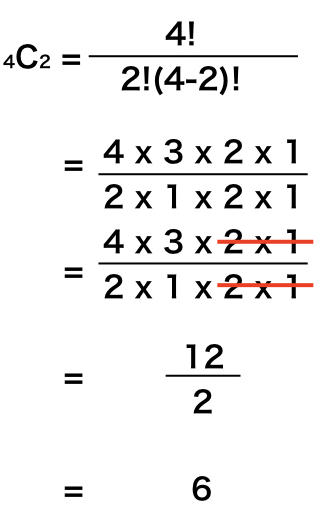



組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



0 件のコメント:
コメントを投稿